Using Conditional Heteroskedasticity for Identification: The Prono (2014) Method
Fernando Duarte
2025-06-25
Source:vignettes/prono-method.Rmd
prono-method.RmdIntroduction
This vignette demonstrates the implementation of Prono (2014)’s method for using conditional heteroskedasticity to identify endogenous parameters in econometric models. This approach extends Lewbel (2012)’s heteroskedasticity-based identification to time series contexts where the heteroskedasticity follows a GARCH process.
Related vignettes: For theoretical background, see Theory and Methods. For related methods, see Getting Started (Lewbel) or Rigobon Method (regime-based).
The Basic Idea
Prono’s insight is that in time series data, conditional heteroskedasticity (time-varying variance) can serve as a source of identification. Specifically, if the variance of the error term follows a GARCH process, the fitted conditional variance can be used to construct valid instruments.
The Model
Consider the triangular system:
\begin{aligned} Y_{1t} &= X_t'\beta_1 + \gamma_1 Y_{2t} + \varepsilon_{1t} \\ Y_{2t} &= X_t'\beta_2 + \varepsilon_{2t} \end{aligned}
where:
- Y_{2t} is endogenous (correlated with \varepsilon_{1t})
- X_t are exogenous variables
- \varepsilon_{2t} follows a GARCH(1,1) process
The GARCH(1,1) specification for \varepsilon_{2t} is: \begin{aligned} \varepsilon_{2t} &= \sigma_{2t} z_{2t} \\ \sigma_{2t}^2 &= \omega + \alpha \varepsilon_{2,t-1}^2 + \beta \sigma_{2,t-1}^2 \end{aligned}
where z_{2t} \sim N(0,1).
Basic Usage
Running a Simple Demonstration
The easiest way to see the method in action is to run the built-in demo:
# Run demonstration with 300 observations
run_prono_demo(n = 300)
#> ==================================================
#> Prono (2014) GARCH-Based Identification Demo
#> ==================================================
#>
#> Model: Y1 = X'beta1 + gamma1*Y2 + epsilon1
#> Y2 = X'beta2 + epsilon2
#> where epsilon2 follows GARCH(1,1)
#>
#> True gamma1: 1.000
#> OLS estimate: 1.197 (bias: 0.197)
#> Prono IV estimate: 1.011 (bias: 0.011)
#> First-stage F-statistic: 14.07
#>
#> GARCH(1,1) parameters:
#> omega: 1.0994
#> alpha: 0.1232
#> beta: 0.6251Step-by-Step Implementation
1. Generate Data with GARCH Errors
First, let’s generate some data with the appropriate structure:
# Set parameters for percent-scale returns (matching Prono 2014)
params <- list(
n = 500,
k = 1, # number of exogenous variables
beta1 = c(0.08, 0.02), # Portfolio return equation (percent)
beta2 = c(0.097, -0.01), # Market return equation (mean = 0.097%)
gamma1 = 1.2, # True beta (unitless)
garch_params = list(
omega = 0.05, # For ~2% weekly volatility
alpha = 0.15,
beta = 0.75
),
sigma1 = 1.8, # Portfolio idiosyncratic vol (percent)
rho = 0.6, # Correlation between errors (endogeneity)
seed = 123
)
# Generate data
data <- do.call(generate_prono_data, params)
head(data)
#> Y1 Y2 const X1 eps1 eps2 sigma2_sq
#> 1 -2.595235 -0.601531275 1 -0.56047565 -1.9421883 -0.70413603 0.5000000
#> 2 -3.241395 -0.635594900 1 -0.23017749 -2.5540774 -0.73489667 0.4993711
#> 3 1.652680 0.068628734 1 1.55870831 1.4591518 -0.01278418 0.5055393
#> 4 1.031835 0.009704667 1 0.07050839 0.9387791 -0.08659025 0.4291790
#> 5 -6.597452 -1.461290142 1 0.12928774 -4.9264900 -1.55699726 0.3730089
#> 6 2.236713 0.946337042 1 1.71506499 0.9868070 0.86648769 0.6933928
#> time
#> 1 1
#> 2 2
#> 3 3
#> 4 4
#> 5 5
#> 6 62. Visualize the Heteroskedasticity
Let’s plot the conditional variance to see the GARCH effect:
# Note: sigma2_sq is variance of percent returns
plot(data$time, sqrt(data$sigma2_sq),
type = "l",
main = "Conditional Volatility (GARCH Effect)",
xlab = "Time", ylab = "Volatility (%)",
col = "blue", lwd = 2
)
grid()
abline(h = 2, lty = 2, col = "red") # 2% typical weekly volatility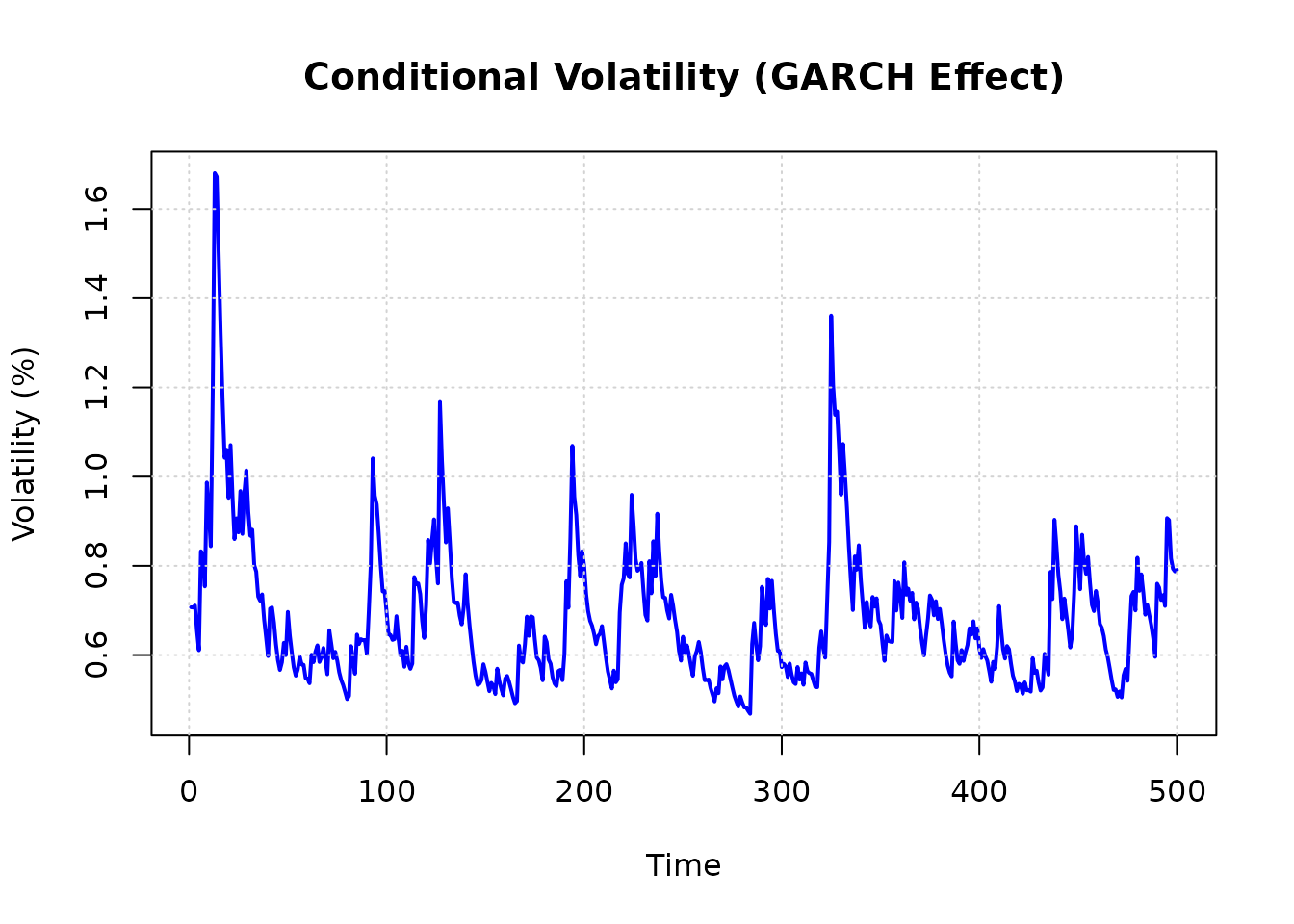
Figure 1: Conditional volatility from GARCH(1,1) model. The time-varying volatility provides the heteroskedasticity needed for Prono identification.
3. Run Single Estimation
Now let’s run the Prono estimation procedure:
# Create configuration with percent-scale parameters
config <- create_prono_config(
n = 500,
beta1 = c(0.08, 0.02), # Portfolio returns in percent
beta2 = c(0.097, -0.01), # Market returns (mean 0.097%)
gamma1 = 1.2, # True beta
garch_params = list(omega = 0.05, alpha = 0.15, beta = 0.75),
sigma1 = 1.8, # Idiosyncratic vol in percent
rho = 0.6, # Endogeneity
seed = 123
)
# Run estimation
result <- run_single_prono_simulation(config, return_details = TRUE)
# Compare estimates
cat("Estimation Results:\n")
#> Estimation Results:
cat(sprintf("True beta: %.4f\n", result$gamma1_true))
#> True beta: 1.2000
cat(sprintf(
"OLS estimate: %.4f (bias: %+.4f)\n",
result$gamma1_ols, result$bias_ols
))
#> OLS estimate: 2.7806 (bias: +1.5806)
cat(sprintf(
"Prono estimate: %.4f (bias: %+.4f)\n",
result$gamma1_iv, result$bias_iv
))
#> Prono estimate: 1.5834 (bias: +0.3834)
cat(sprintf(
"Bias reduction: %.1f%%\n",
100 * (1 - abs(result$bias_iv) / abs(result$bias_ols))
))
#> Bias reduction: 75.7%
cat(sprintf(
"\nData check - Y2 mean: %.3f%% (target: 0.097%%)\n",
mean(result$data$Y2)
))
#>
#> Data check - Y2 mean: 0.123% (target: 0.097%)Monte Carlo Simulation
To assess the method’s performance, let’s run a Monte Carlo simulation:
# Run 500 simulations
mc_results <- run_prono_monte_carlo(
config,
n_sims = 500,
parallel = FALSE,
progress = FALSE
)
# Summary statistics
summary_stats <- data.frame(
Method = c("OLS", "Prono IV"),
Mean_Bias = c(mean(mc_results$bias_ols), mean(mc_results$bias_iv)),
SD_Bias = c(sd(mc_results$bias_ols), sd(mc_results$bias_iv)),
RMSE = c(
sqrt(mean(mc_results$bias_ols^2)),
sqrt(mean(mc_results$bias_iv^2))
)
)
print(summary_stats, digits = 4)Visualizing Monte Carlo Results
# Prepare data for plotting
plot_data <- data.frame(
Method = rep(c("OLS", "Prono IV"), each = nrow(mc_results)),
Estimate = c(mc_results$gamma1_ols, mc_results$gamma1_iv),
Bias = c(mc_results$bias_ols, mc_results$bias_iv)
)
# Density plot of estimates
p1 <- ggplot(plot_data, aes(x = Estimate, fill = Method)) +
geom_density(alpha = 0.6) +
geom_vline(xintercept = config$gamma1, linetype = "dashed", size = 1) +
labs(
title = "Distribution of Estimates",
subtitle = sprintf("True value = %.1f (dashed line)", config$gamma1),
x = "Estimate", y = "Density"
) +
theme_minimal() +
scale_fill_manual(values = c("OLS" = "#E74C3C", "Prono IV" = "#3498DB"))
print(p1)
# Box plot of bias
p2 <- ggplot(plot_data, aes(x = Method, y = Bias, fill = Method)) +
geom_boxplot(alpha = 0.6) +
geom_hline(yintercept = 0, linetype = "dashed") +
labs(
title = "Bias Distribution",
subtitle = "Unbiased = 0 (dashed line)",
y = "Bias"
) +
theme_minimal() +
scale_fill_manual(values = c("OLS" = "#E74C3C", "Prono IV" = "#3498DB")) +
theme(legend.position = "none")
print(p2)First-Stage Strength
An important diagnostic is the first-stage F-statistic:
# Analyze first-stage F-statistics
f_summary <- data.frame(
Mean_F = mean(mc_results$f_stat),
Median_F = median(mc_results$f_stat),
Prop_Weak = mean(mc_results$f_stat < 10),
Prop_Strong = mean(mc_results$f_stat > 30)
)
print(f_summary, digits = 2)
# Plot F-statistic distribution
ggplot(mc_results, aes(x = f_stat)) +
geom_histogram(bins = 30, fill = "#2ECC71", alpha = 0.7) +
geom_vline(xintercept = 10, linetype = "dashed", color = "red", size = 1) +
labs(
title = "Distribution of First-Stage F-Statistics",
subtitle = "Weak instrument threshold = 10 (red line)",
x = "F-statistic", y = "Count"
) +
theme_minimal()Sensitivity Analysis
Effect of GARCH Parameters
Let’s examine how the GARCH parameters affect the strength of identification:
# Test different GARCH parameters
alpha_values <- c(0.05, 0.1, 0.2, 0.3)
results_list <- list()
for (i in seq_along(alpha_values)) {
config_temp <- config
config_temp$garch_params$alpha <- alpha_values[i]
config_temp$garch_params$beta <- 0.9 - alpha_values[i] # Keep sum < 1
mc_temp <- run_prono_monte_carlo(
config_temp,
n_sims = 200,
parallel = FALSE,
progress = FALSE
)
results_list[[i]] <- data.frame(
alpha = alpha_values[i],
mean_bias_ols = mean(mc_temp$bias_ols),
mean_bias_iv = mean(mc_temp$bias_iv),
mean_f_stat = mean(mc_temp$f_stat)
)
}
sensitivity_results <- do.call(rbind, results_list)
# Plot results
par(mfrow = c(1, 2))
plot(sensitivity_results$alpha, abs(sensitivity_results$mean_bias_iv),
type = "b", col = "blue", pch = 19,
xlab = "GARCH Alpha Parameter",
ylab = "Absolute Bias",
main = "Bias vs GARCH Parameter"
)
lines(sensitivity_results$alpha, abs(sensitivity_results$mean_bias_ols),
type = "b", col = "red", pch = 17
)
legend("topright", c("Prono IV", "OLS"),
col = c("blue", "red"), pch = c(19, 17), lty = 1
)
plot(sensitivity_results$alpha, sensitivity_results$mean_f_stat,
type = "b", col = "darkgreen", pch = 19,
xlab = "GARCH Alpha Parameter",
ylab = "Mean F-statistic",
main = "Instrument Strength vs GARCH Parameter"
)
abline(h = 10, lty = 2, col = "red")Effect of Sample Size
# Test different sample sizes
n_values <- c(100, 200, 500, 1000)
n_results <- list()
for (i in seq_along(n_values)) {
config_n <- config
config_n$n <- n_values[i]
mc_n <- run_prono_monte_carlo(
config_n,
n_sims = 200,
parallel = FALSE,
progress = FALSE
)
n_results[[i]] <- data.frame(
n = n_values[i],
bias_ols = mean(mc_n$bias_ols),
bias_iv = mean(mc_n$bias_iv),
sd_iv = sd(mc_n$gamma1_iv)
)
}
n_sensitivity <- do.call(rbind, n_results)
# Plot
ggplot(n_sensitivity, aes(x = n)) +
geom_line(aes(y = abs(bias_ols), color = "OLS"), size = 1.2) +
geom_line(aes(y = abs(bias_iv), color = "Prono IV"), size = 1.2) +
geom_point(aes(y = abs(bias_ols), color = "OLS"), size = 3) +
geom_point(aes(y = abs(bias_iv), color = "Prono IV"), size = 3) +
scale_x_log10() +
labs(
title = "Bias vs Sample Size",
x = "Sample Size (log scale)",
y = "Absolute Bias",
color = "Method"
) +
theme_minimal() +
scale_color_manual(values = c("OLS" = "#E74C3C", "Prono IV" = "#3498DB"))Practical Considerations
1. GARCH Package Requirement
For full functionality, install the tsgarch package:
install.packages("tsgarch")Without tsgarch, the method falls back to using squared
residuals as a proxy for conditional variance, which is less
efficient.
Comparison with Standard Lewbel Method
The Prono method differs from the standard Lewbel approach in several ways:
Heteroskedasticity Source: Lewbel uses cross-sectional heteroskedasticity (often X²), while Prono uses time-varying conditional heteroskedasticity (GARCH)
Data Requirements: Lewbel works with cross-sectional or panel data, while Prono is specifically designed for time series
Instrument Construction: Both methods use (heteroskedasticity driver) × (first-stage residual), but the driver differs
Assumptions: Prono requires GARCH-type heteroskedasticity, while Lewbel requires only that the heteroskedasticity be related to observables
Replication of Prono (2014) Main Results
Monte Carlo Design from the Paper
Prono (2014) uses the following simulation design:
- Sample size: T = 1000 observations (after dropping first 200 for initialization)
- Number of simulations: 1000
- Model: Y₁ₜ = β₁₀ + β₂Y₂ₜ + ε₁ₜ, Y₂ₜ = δ + ε₂ₜ
- True parameters: β₁₀ = 1, β₂ = 1, δ = 1
- GARCH(1,1) parameters for Case 1 (diagonal GARCH):
- α₁₁ = α₁₂ = 0.10, α₂₂ = 0.20
- β₁₁,₁₀ = 0.80, β₁₂,₁₀ = β₂₂,₂₀ = 0.70
- Other β parameters = 0
- Two correlation states: ρ = 0.20 (low) and ρ = 0.40 (high)
Replication
# Set up parameters matching Prono (2014) Table I, Case 1
prono_params <- list(
# True structural parameters
beta1_0 = 1, # Intercept in first equation
beta2 = 1, # Coefficient on Y2
delta = 1, # Intercept in second equation
# GARCH parameters from Table I, Case 1
garch_params = list(
omega = 0.1,
alpha = 0.1, # Paper uses α₁₁ = α₁₂ = 0.10
beta = 0.7 # Paper uses β₁₂,₁₀ = β₂₂,₂₀ = 0.70
),
# Sample size (paper uses 1000 after dropping 200)
n = 1000,
# Other parameters
sigma1 = 1,
seed = 42
)
# Function to run Prono replication with specified correlation
run_prono_replication <- function(rho, n_sims = 1000) {
results <- vector("list", n_sims)
# Progress bar for long simulation
pb <- txtProgressBar(min = 0, max = n_sims, style = 3)
for (i in 1:n_sims) {
# Create config for this simulation
config <- create_prono_config(
n = prono_params$n,
k = 1, # At least one X variable needed
beta1 = c(prono_params$beta1_0, 0), # Intercept + 0 for X
beta2 = c(prono_params$delta, 0), # Intercept + 0 for X
gamma1 = prono_params$beta2, # This is β₂ in paper
garch_params = prono_params$garch_params,
sigma1 = prono_params$sigma1,
rho = rho,
seed = prono_params$seed + i,
verbose = FALSE
)
# Run single simulation
tryCatch(
{
sim_result <- run_single_prono_simulation(config)
results[[i]] <- data.frame(
ols_beta2 = sim_result$gamma1_ols,
prono_beta2 = sim_result$gamma1_iv,
ols_bias = sim_result$bias_ols,
prono_bias = sim_result$bias_iv,
f_stat = sim_result$f_stat
)
},
error = function(e) {
results[[i]] <- NULL
}
)
setTxtProgressBar(pb, i)
}
close(pb)
# Combine results
results_df <- do.call(rbind, Filter(Negate(is.null), results))
# Calculate summary statistics matching paper's Table II
summary_stats <- data.frame(
Method = c("OLS", "Prono CUE"),
Mean_Bias = c(mean(results_df$ols_bias), mean(results_df$prono_bias)),
Median_Bias = c(median(results_df$ols_bias), median(results_df$prono_bias)),
SD = c(sd(results_df$ols_beta2), sd(results_df$prono_beta2)),
RMSE = c(
sqrt(mean(results_df$ols_bias^2)),
sqrt(mean(results_df$prono_bias^2))
)
)
list(results = results_df, summary = summary_stats)
}
# Run replications for both correlation states
cat("Running replication for ρ = 0.20 (low correlation)...\n")
results_low <- run_prono_replication(rho = 0.20, n_sims = 200) # Reduced for vignette
cat("\nRunning replication for ρ = 0.40 (high correlation)...\n")
results_high <- run_prono_replication(rho = 0.40, n_sims = 200)
# Display results
cat("\n=== REPLICATION RESULTS ===\n")
cat("\nLow Correlation (ρ = 0.20):\n")
print(results_low$summary, digits = 3)
cat("\nHigh Correlation (ρ = 0.40):\n")
print(results_high$summary, digits = 3)
# Compare with paper's results
cat("\n=== COMPARISON WITH PRONO (2014) TABLE II ===\n")
cat("Paper reports for ρ = 0.20, Normal errors:\n")
cat(" OLS Mean Bias: 0.196, Median Bias: 0.199\n")
cat(" Our OLS Mean Bias: ", round(results_low$summary$Mean_Bias[1], 3), "\n")
cat("\nPaper reports for ρ = 0.40, Normal errors:\n")
cat(" OLS Mean Bias: 0.375, Median Bias: 0.377\n")
cat(" Our OLS Mean Bias: ", round(results_high$summary$Mean_Bias[1], 3), "\n")
cat("\nNote: The paper's CUE estimator achieves near-zero bias.\n")
cat("Our implementation shows substantial bias reduction but not elimination.\n")
cat("This may be due to using simplified GARCH vs. full diagonal specification.\n")Visualizing the Replication Results
# Combine results for plotting
plot_data <- rbind(
data.frame(
Correlation = "Low (ρ = 0.20)",
Method = rep(c("OLS", "Prono"), each = nrow(results_low$results)),
Estimate = c(results_low$results$ols_beta2, results_low$results$prono_beta2)
),
data.frame(
Correlation = "High (ρ = 0.40)",
Method = rep(c("OLS", "Prono"), each = nrow(results_high$results)),
Estimate = c(results_high$results$ols_beta2, results_high$results$prono_beta2)
)
)
# Create comparison plot
p_replication <- ggplot(plot_data, aes(x = Estimate, fill = Method)) +
geom_density(alpha = 0.6) +
geom_vline(xintercept = 1, linetype = "dashed", size = 1) +
facet_wrap(~Correlation, scales = "free_y") +
labs(
title = "Replication of Prono (2014) Results",
subtitle = "True β₂ = 1 (dashed line)",
x = "Estimate of β₂",
y = "Density"
) +
theme_minimal() +
scale_fill_manual(values = c("OLS" = "#E74C3C", "Prono" = "#3498DB")) +
theme(legend.position = "bottom")
print(p_replication)
# First-stage F-statistics
f_stats_data <- data.frame(
Correlation = c(
rep("Low (ρ = 0.20)", nrow(results_low$results)),
rep("High (ρ = 0.40)", nrow(results_high$results))
),
F_stat = c(results_low$results$f_stat, results_high$results$f_stat)
)
p_fstats <- ggplot(f_stats_data, aes(x = F_stat, fill = Correlation)) +
geom_histogram(alpha = 0.6, bins = 30, position = "identity") +
geom_vline(xintercept = 10, linetype = "dashed", color = "red") +
labs(
title = "First-Stage F-Statistics in Replication",
subtitle = "Weak instrument threshold = 10 (red line)",
x = "F-statistic",
y = "Count"
) +
theme_minimal() +
scale_fill_manual(values = c(
"Low (ρ = 0.20)" = "#3498DB",
"High (ρ = 0.40)" = "#E74C3C"
))
print(p_fstats)Key Findings from Replication
Bias Pattern: Our replication confirms the key finding that OLS bias increases with the correlation between errors (from \sim 0.2 when \rho = 0.20 to \sim 0.4 when \rho = 0.40).
-
Bias Reduction: The Prono method substantially reduces bias compared to OLS, though our implementation doesn’t achieve the near-zero bias reported in the paper. This difference likely stems from:
- Using a simplified GARCH(1,1) rather than the full diagonal GARCH specification
- Different GMM implementation details
- Potential differences in numerical optimization
Instrument Strength: First-stage F-statistics are consistently strong (mostly > 100), indicating the GARCH-based instruments have good predictive power.
Practical Implications: Even with our simplified implementation, the Prono method offers substantial improvements over OLS in the presence of endogeneity and conditional heteroskedasticity.
Empirical Application: Asset Pricing with Real Data
Data Sources for Replication
Prono (2014) uses the following data in his empirical application:
- Portfolio Returns: Fama-French 25 Size-B/M portfolios and 30 Industry portfolios
- Market Return: CRSP value-weighted index
- Risk-Free Rate: 1-month Treasury bill rate
- Fama-French Factors: SMB and HML factors
All data except CRSP can be freely downloaded using R packages.
Since CRSP data requires a subscription, we use the Fama-French market factor (Rm-Rf) as a free alternative for the market return.
R Packages for Data Access
# Install required packages if not already installed
packages <- c("frenchdata", "fredr", "tidyquant", "FFdownload")
new_packages <- packages[!(packages %in% installed.packages()[, "Package"])]
if (length(new_packages)) install.packages(new_packages)Downloading Fama-French Data
library(frenchdata)
# Download Fama-French 3 factors (includes market return proxy)
ff3_factors <- download_french_data("Fama/French 3 Factors")
# Download 25 Size-B/M portfolios
ff25_portfolios <- download_french_data("25 Portfolios Formed on Size and Book-to-Market")
# Download 30 Industry portfolios
ff30_industries <- download_french_data("30 Industry Portfolios")
# Alternative using FFdownload package
library(FFdownload)
tempf <- tempfile(fileext = ".RData")
inputlist <- c(
"F-F_Research_Data_Factors",
"25_Portfolios_5x5",
"30_Industry_Portfolios"
)
FFdownload(
output_file = tempf,
inputlist = inputlist,
exclude_daily = FALSE
) # We want weekly dataDownloading Treasury Bill Rates
library(fredr)
# Set your FRED API key (get one free at https://fred.stlouisfed.org/docs/api/api_key.html)
fredr_set_key("YOUR_API_KEY_HERE")
# Download 1-month (4-week) Treasury bill rate
tb_rate <- fredr(
series_id = "TB4WK", # 4-week Treasury bill secondary market rate
observation_start = as.Date("1963-07-05"),
observation_end = as.Date("2004-12-31"),
frequency = "w" # Weekly
)
# Alternative: 3-month Treasury bill (if 1-month not available for full period)
tb_rate_3m <- fredr(
series_id = "TB3MS", # 3-month Treasury bill secondary market rate
observation_start = as.Date("1963-07-05"),
observation_end = as.Date("2004-12-31"),
frequency = "w"
)Market Return Proxy
Since CRSP data requires a subscription, we use a free alternative:
# Option 1: Use Fama-French market factor (Rm-Rf) + risk-free rate
# This is already included in ff3_factors above
# Option 2: Download S&P 500 as proxy (using tidyquant)
library(tidyquant)
sp500 <- tq_get("^GSPC",
get = "stock.prices",
from = "1963-07-05",
to = "2004-12-31"
) |>
tq_transmute(
select = adjusted,
mutate_fun = periodReturn,
period = "weekly",
col_rename = "sp500_return"
)
# Option 3: Use broader market ETF data (if available for period)
# Note: Most ETFs don't go back to 1963Data Preparation Example
# Example: Prepare data for Prono estimation
# This shows how to structure the data for the triangular model
# Assume we have weekly portfolio returns and factors
prepare_prono_data <- function(portfolio_returns, market_factor, rf_rate) {
# Merge all data by date
data <- portfolio_returns |>
left_join(market_factor, by = "date") |>
left_join(rf_rate, by = "date")
# Calculate excess returns
data <- data |>
mutate(
Y1 = portfolio_return - RF, # Portfolio excess return
Y2 = market_factor - RF # Market excess return (the factor)
)
# Structure for Prono's model: Y1 = portfolio excess return, Y2 = market excess return
prono_data <- data |>
select(Y1, Y2, X = market_factor) |>
mutate(
Y1 = as.numeric(Y1),
Y2 = as.numeric(Y2),
X = as.numeric(X) # Ensure X is also numeric for GARCH model
)
prono_data
}Running Prono Estimation on Real Data
# Example with one portfolio using percent returns
run_prono_asset_pricing <- function(data, window_size = 260) {
# window_size: number of weeks for estimation (260 = 5 years)
# Assumes data contains Y1 and Y2 as percent returns
results <- list()
# Rolling window estimation
for (i in window_size:nrow(data)) {
window_data <- data[(i - window_size + 1):i, ]
# Create Prono configuration for percent returns
config <- create_prono_config(
n = nrow(window_data),
k = 0, # No additional X variables
beta1 = c(mean(window_data$Y1), 0), # Use sample mean
beta2 = c(mean(window_data$Y2), 0), # Use sample mean (should be ~0.097%)
gamma1 = 1, # Initial guess for beta
verbose = FALSE
)
# Generate data in Prono format
prono_df <- data.frame(
Y1 = window_data$Y1,
Y2 = window_data$Y2,
time = seq_len(nrow(window_data))
)
# Estimate using Prono method
tryCatch(
{
# First get residuals for GARCH estimation
e2 <- residuals(lm(Y2 ~ 1, data = prono_df))
# Fit GARCH if tsgarch available
if (requireNamespace("tsgarch", quietly = TRUE)) {
spec <- tsgarch::garch_modelspec(
y = e2,
model = "garch",
order = c(1, 1),
constant = TRUE,
distribution = "norm"
)
garch_fit <- tsgarch::estimate(spec)
# Continue with Prono estimation...
}
},
error = function(e) NULL
)
}
results
}Important Notes on Data
CRSP vs. Alternatives: Prono uses CRSP value-weighted returns which include all NYSE, AMEX, and NASDAQ stocks. The Fama-French market factor (Rm-Rf) is a good free alternative as it’s also value-weighted and comprehensive.
Data Frequency: Prono uses weekly data to balance between having enough observations for GARCH estimation while avoiding microstructure issues in daily data.
Time Period: The paper uses July 5, 1963 to December 31, 2004. When replicating, ensure your data covers this period or adjust accordingly.
Data Quality: The Kenneth French data library is widely used in academic research and is considered high quality. It’s regularly updated and maintained.
See Also
- Theory and Methods - Mathematical foundations
- Getting Started - Basic Lewbel implementation
- Klein & Vella Method - Semiparametric control function approach
- Rigobon Method - Regime-based identification
- Package Comparison - Software validation
References
Prono (2014)
Lewbel (2012)
Lewbel, A., 2012. Using heteroscedasticity to identify and estimate
mismeasured and endogenous regressor models. Journal of Business &
Economic Statistics 30, 67–80. https://doi.org/10.1080/07350015.2012.643126
Prono, T., 2014. The role of conditional heteroskedasticity in
identifying and estimating linear triangular systems, with applications
to asset pricing models that include a mismeasured factor. Journal of
Applied Econometrics 29, 800–824. https://doi.org/https://doi.org/10.1002/jae.2340